Back propagation in Pure Python

Back propagation is a important concept in machine learning. It is a method to train a neural network. In this article, I will show you how to implement a simple back propagation in Pure Python.

Back propagation concept

First, we need to calculate the error of the neural network. The error is the difference between the predicted value and the actual value. Then, we need to update the weights of the neural network. The weights are updated by the error and the learning rate.

For example, let's say we have a neural network with one neuron and one input. The neural network is defined as follows:

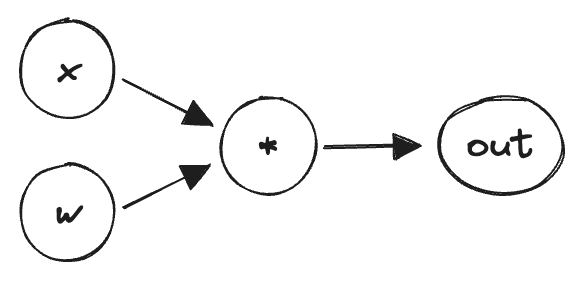
This has x as input, w as weight and out as output.

Forward pass

Forward pass is the process of calculating the output of the neural network. In this case, the output is $w\cdot x$.

Error calculation

Error calculation is the process of calculating the difference between the predicted value and the actual value. In this example, we use Mean Squared Error as the error function. (For every input, we calculate the error and take the average.)

Error Calculation:
$err=\left(\frac{1}{N}\right){(out-y)}^2$
Total Error:
$err=\sum _i^N\left(\frac{1}{N}\right){(ou{t}_i-y_i)}^2$

Gradient Descent Approach

Gradient Descent is an optimization algorithm used to minimize some function by iteratively moving in the direction of steepest descent as defined by the negative of the gradient. - ChatGPT

The new weight is calculated as follows:

$\left(w^{\star }\right)=w-\alpha \times (\partial err)/(\partial w)$

Where $\alpha$ is the learning rate and $w^{\star }$ is the updated weight.

Implementation

Defining the neural network

X: list[float] = [1, 2, 3, 4] # Input
Y: list[float] = [2, 4, 6, 8] # Expected output

w = 0.0              # Arbitrary initial weight
learning_rate = 0.01 # Learning rate
n_iters = 10         # Number of iterations

Modal Prediction

In this example, our forward pass is $w\times x$.

def forward(x):
    if not isinstance(x, list):
        x = [x]
    return w * x

Loss Calculation (MSE Error)

$\text{LOSS}=\left(\frac{1}{N}\right)\sum _i^N{(y{p}_i-y_i)}^2$

def loss(y, y_pred):
    return sum((yp-yi)**2 for yp, yi in zip(y_pred, y)) / len(y)

Gradient Calculation

$(\partial err)/(\partial w)=\partial \left(\frac{{(wx-y)}^2}{N}\right)/\partial w=\frac{2x(wx-y)}{N}=\frac{2x(yp-y)}{N}$

def gradient(x, y, y_pred):
    return sum(2 * (yp - yi) * xi for xi, yp, yi in zip(x, y_pred, y)) / len(y)

Training

for epoch in range(n_iters):
    y_pred = forward(X)

    # loss
    l = loss(Y, y_pred)

    # gradient
    dw = gradient(X, Y, y_pred)

    # update weight
    w -= learning_rate * dw

    print(f"epoch {epoch + 1}: w = {w:.3f}, loss = {l:.8f}")

print(f"Prediction after training: f(5) = {forward(5)[0]:.3f}")

Output

Prediction before training: f(5) = 0.0
epoch 1: w = 0.300, loss = 30.00000000
epoch 2: w = 0.555, loss = 21.67500000
epoch 3: w = 0.772, loss = 15.66018750
epoch 4: w = 0.956, loss = 11.31448547
epoch 5: w = 1.113, loss = 8.17471575
epoch 6: w = 1.246, loss = 5.90623213
epoch 7: w = 1.359, loss = 4.26725271
epoch 8: w = 1.455, loss = 3.08309009
epoch 9: w = 1.537, loss = 2.22753259
epoch 10: w = 1.606, loss = 1.60939229
Prediction after training: f(5) = 8.031